
“Nella scienza esiste solo la Fisica; tutto il resto è collezione di francobolli.”
— Ernest Rutherford
La teoria del Nobel Giorgio Parisi sulla via ottimale dell’informatica quantistica sta suscitando grande interesse nel mondo scientifico. In questo articolo esploreremo i concetti chiave dell’intelligenza artificiale e dell’informatica quantistica, e come la tecnica del quantum annealing possa rivoluzionare il campo. Vedremo inoltre come il calcolo quantistico possa risolvere problemi complessi in modo più efficiente, e quali vantaggi l’annealing quantistico offra nell’ottimizzazione del calcolo. Infine, discuteremo le sfide che devono ancora essere affrontate e il futuro promettente dell’informatica quantistica.
L’intelligenza artificiale e l’informatica quantistica
L’intelligenza artificiale e l’informatica quantistica sono due ambiti di ricerca che stanno sempre più convergendo, aprendo nuove prospettive e sfide. L’intelligenza artificiale si basa sull’utilizzo di algoritmi complessi per simulare il pensiero umano e migliorare le capacità delle macchine nell’apprendimento e nella risoluzione di problemi. D’altra parte, l’informatica quantistica si occupa dello sviluppo di algoritmi che sfruttano i principi della meccanica quantistica per eseguire calcoli più rapidamente rispetto ai computer classici. L’obiettivo è quello di sfruttare le proprietà dei qubit, unità di informazione quantistica, per risolvere problemi complessi in modo più efficiente. La combinazione di intelligenza artificiale e informatica quantistica può portare a importanti avanzamenti in diversi settori, come la medicina, la crittografia e la simulazione molecolare. Tuttavia, ci sono ancora molte sfide da affrontare, come l’instabilità dei qubit e la necessità di algoritmi adeguati per sfruttare appieno le potenzialità dell’informatica quantistica.
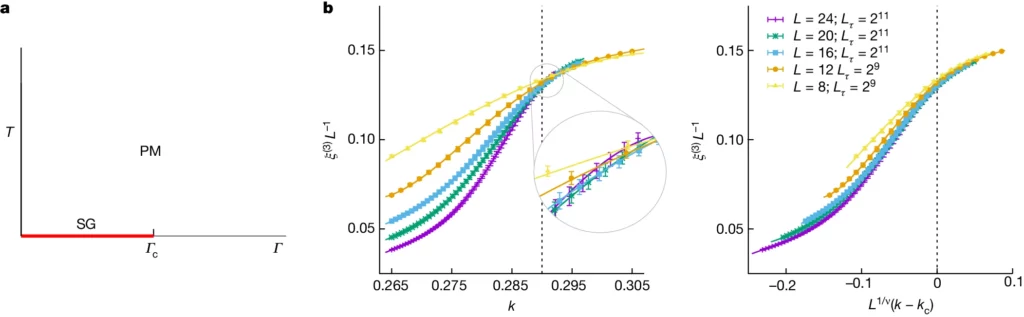
a, diagramma di fase per un vetro di spin Ising bidimensionale in termini di temperatura T e campo trasversale Γ. Per tutti i T > 0, il sistema è disordinato se studiato a grandi scale di lunghezza, quindi si trova nella fase paramagnetica (PM). A T = 0, lo stato fondamentale appare disordinato per Γ > Γc (dal punto di vista della base computazionale). Per Γ < Γc, incontriamo la fase spin-glass (SG), che è diversa per ogni realizzazione di disordine. b, la nostra analisi di scala finite-size del punto critico a T = 0 e Γ = Γc, in termini del parametro k che rappresenta Γ nella formulazione di Trotter-Suzuki ("La formula di Trotter-Suzuki" in Metodi; k cresce al diminuire di Γ). A sinistra, lunghezza di correlazione ξ(3) in unità della dimensione del reticolo L rispetto a k. Le curve per i diversi L si intersecano nel punto critico kc ≈ 0,29. A destra, i dati nel pannello di sinistra di b, rappresentati in funzione della variabile scalare L1/ν(k - kc) con 1/ν = 0,7, convergono verso una curva limite al crescere di L. I punti in b sono medie statistiche, con un'approssimazione di k. I punti in b sono medie statistiche e gli errori corrispondono a una deviazione standard.
Il quantum annealing: una tecnica rivoluzionaria
Il quantum annealing è una tecnica rivoluzionaria nell’ambito dell’informatica quantistica che promette di risolvere problemi complessi in modo efficiente. Questo approccio si basa sull’utilizzo di qubit, unità di informazione quantistica, per esplorare tutte le possibili soluzioni di un problema contemporaneamente. A differenza dei classici algoritmi computazionali, che esaminano sequenzialmente le varie opzioni, il quantum annealing può trovare la soluzione ottimale in tempi molto più brevi. Questa tecnica si avvale del principio dell’annealing, un processo di raffreddamento controllato che permette ai qubit di raggiungere uno stato di minima energia corrispondente alla soluzione cercata. Il quantum annealing ha dimostrato grandi potenzialità nell’ottimizzazione del calcolo, trovando applicazioni in settori come la logistica, l’intelligenza artificiale e la ricerca farmaceutica. La sua capacità di superare i limiti dei computer classici apre nuove prospettive per la risoluzione di problemi complessi e stimola ulteriori ricerche nello sviluppo dell’informatica quantistica.
Risolvere problemi complessi con il calcolo quantistico
Risolvere problemi complessi con il calcolo quantistico è uno dei principali obiettivi dell’informatica quantistica. Mentre i computer classici utilizzano bit per rappresentare l’informazione, i computer quantistici sfruttano qubit, che possono esistere in più stati contemporaneamente grazie al principio di sovrapposizione quantistica. Questo permette ai computer quantistici di esplorare diverse soluzioni simultaneamente, accelerando notevolmente la risoluzione di problemi complessi. Ad esempio, l’algoritmo di Grover utilizza il calcolo quantistico per cercare una soluzione in un database non ordinato in modo efficiente, riducendo il tempo necessario rispetto all’algoritmo classico. Inoltre, il calcolo quantistico può essere utilizzato per la simulazione di sistemi fisici complessi, come ad esempio molecole o materiali, fornendo risultati più accurati rispetto alle simulazioni classiche. Nonostante le sfide tecniche ancora da affrontare, il calcolo quantistico promette di rivoluzionare la risoluzione di problemi complessi in vari settori, dall’ottimizzazione alla crittografia.
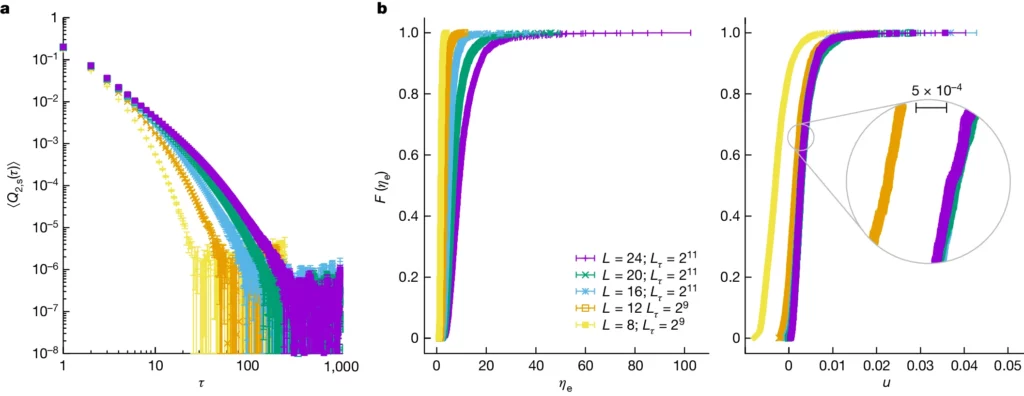
a, la funzione di correlazione sottratta mediata dal campione Q2,s(τ) ("Processo di adattamento e stima della lunghezza di correlazione euclidea) diventa compatibile con lo zero per valori moderati di τ, per tutte le dimensioni del nostro sistema. b, a sinistra, dopo aver calcolato la lunghezza di correlazione euclidea per ogni campione, abbiamo calcolato per ogni L la funzione di distribuzione empirica F(ηe), ossia la probabilità F di trovare un campione con (notare le barre di errore orizzontali). A destra, i dati nel pannello di sinistra di b, quando sono tracciati in funzione della variabile di scala u, non mostrano alcuna dipendenza dal residuo L, tranne che per le nostre dimensioni più piccole L = 8 e 12. I punti in a e b sono medie statistiche e gli errori corrispondono a una deviazione standard.
I vantaggi dell’annealing quantistico nell’ottimizzazione del calcolo
L’annealing quantistico offre numerosi vantaggi nell’ottimizzazione del calcolo. A differenza dei tradizionali algoritmi classici, l’annealing quantistico sfrutta le proprietà della meccanica quantistica per esplorare in modo efficiente le possibili soluzioni di un problema. Questa tecnica consente di superare i limiti delle soluzioni classiche, permettendo di risolvere problemi complessi in tempi molto più brevi. Grazie alla sua capacità di esplorare simultaneamente diverse soluzioni, l’annealing quantistico può trovare rapidamente la soluzione ottimale tra un vasto numero di possibilità. Inoltre, questa tecnica è particolarmente efficace nella ricerca di minime globali, consentendo di evitare le trappole locali che possono rallentare il processo di ottimizzazione. Con questi vantaggi, l’annealing quantistico si sta rivelando una promettente strada per migliorare l’efficienza e la velocità del calcolo ottimizzato.
Superando le sfide: il futuro dell’informatica quantistica
Il futuro dell’informatica quantistica è pieno di sfide e opportunità. Una delle principali sfide è quella di sviluppare hardware quantistico più potente e stabile. Attualmente, i computer quantistici sono ancora molto sensibili all’errore e richiedono ambienti estremamente controllati per funzionare correttamente. Tuttavia, gli scienziati stanno facendo progressi significativi nello sviluppo di tecnologie che riducono l’errore e aumentano la stabilità dei qubit, i mattoni fondamentali del calcolo quantistico. Un’altra sfida importante è quella di sviluppare algoritmi e software adatti all’informatica quantistica. Gli algoritmi classici spesso non sono ottimizzati per l’uso sui computer quantistici, quindi è necessario svilupparne di nuovi che sfruttino appieno le caratteristiche uniche di questa tecnologia. Nonostante queste sfide, il futuro dell’informatica quantistica sembra promettente. L’uso dell’informatica quantistica potrebbe portare a scoperte scientifiche rivoluzionarie, soluzioni ottimali per problemi complessi e miglioramenti significativi in settori come la sicurezza informatica e la simulazione molecolare.
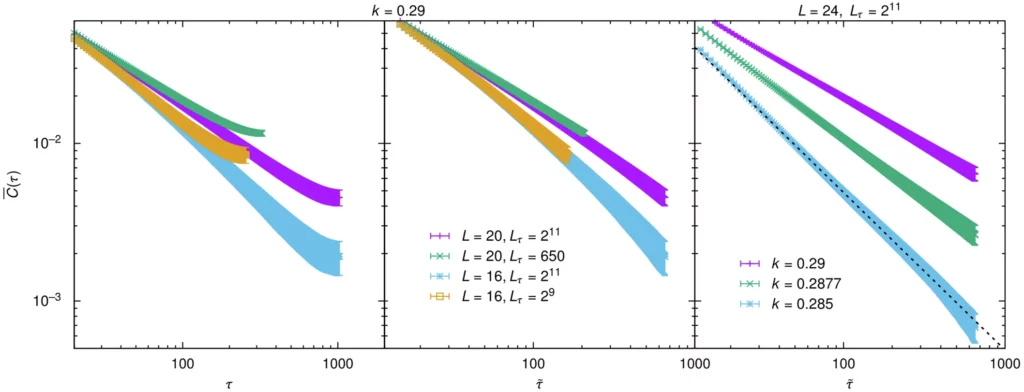
Funzione di correlazione euclidea mediata per campione in funzione della distanza euclidea τ (pannello di sinistra), per evitare distorsioni dovute alle condizioni periodiche al contorno (pannelli centrale e destro). I pannelli a sinistra e al centro mostrano la dipendenza dalle dimensioni del sistema per k = 0,29, mentre il pannello a destra mostra la dipendenza da k per il sistema più grande, L = 24 e Lτ = 211. La linea tratteggiata nel pannello di destra è una guida per l'occhio per mostrare l'esponente critico incontrato per k = 0,285. I punti sono medie statistiche e gli errori corrispondono a una deviazione standard.
Bernaschi, M., González-Adalid Pemartín, I., Martín-Mayor, V. et al. The quantum transition of the two-dimensional Ising spin glass. Nature (2024). https://doi.org/10.1038/s41586-024-07647-y
In conclusione…
L’intelligenza artificiale e l’informatica quantistica stanno aprendo nuove frontiere nel campo del calcolo e della risoluzione dei problemi complessi. Il quantum annealing, una tecnica rivoluzionaria, sta dimostrando di essere estremamente promettente nell’ottimizzazione del calcolo. Grazie alle sue caratteristiche uniche, come la capacità di esplorare molteplici soluzioni simultaneamente, l’annealing quantistico offre vantaggi significativi rispetto ai tradizionali algoritmi di ottimizzazione. Tuttavia, ci sono ancora sfide da affrontare per rendere l’informatica quantistica una realtà pratica su larga scala. Il futuro dell’informatica quantistica richiederà sforzi continui per superare queste sfide e sviluppare nuove tecniche e tecnologie. Come sarà il mondo con l’informatica quantistica? Cosa significa per il futuro dell’intelligenza artificiale e della nostra società? Queste domande rimangono aperte e invitano a ulteriori riflessioni sul potenziale e le implicazioni dell’informatica quantistica.





